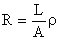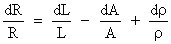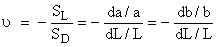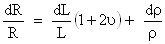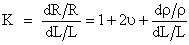|
|
||
|
Fundamentals of piezoresistive conversion
Basic resistivity relationships
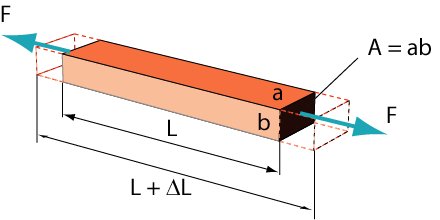
Case of a long solid bar
where L is the length, A is the cross-section and r is the resistivity of the material
Two components of the piezoresistive effect
With the aid of Poisson ratio, n defined as the relative increase in the length SL to the relative decrease in the diameter SD (or a or b)
In metals, the gauge factor is defined mostly by the geometric component which is expressed by two first members of the preceding expression For this reason, the gauge factors of metals are rather small and attain the values between 2 and 4.
Gauge factor of semiconductors is much higher Doped silicon exhibits a gauge factor which can be as large as 200, depending on the amount of doping This effect is the result of the resistive component corresponding to the third member of the preceding expression
|
 Accelerometer
Accelerometer