 |
|
||
|
For OZ direction one considers a charge distribution of The potentials are
Taking into account those mentioned above and using a new superposition, the residual potential of the T-branch will be:
For a deeper research in practice, bellow are offered [2] a few approximations of the T-branch parameters, excellent formulas for some discontinuities in microstrip configurations being offered by the famous scientist Gupta. The approximations are included in the lumped equivalent circuit model presented in figure 2 for particular conditions of characteristic impedance (Z0=50W) and substrate (Al2O3, er=9,9). The inductances of the two arms can be evaluated very similar as in the case of the corner discontinuity.
|
 Schematic design of PCB projects
Schematic design of PCB projects 
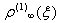 of an infinite line and other two of
of an infinite line and other two of 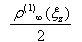 with reversed polarities in the point z = {-1,1}.
with reversed polarities in the point z = {-1,1}.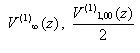 and
and 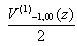 . Them superposition produces on intervals zÎ(1,+¥) şi zÎ(-¥, -1) the following potential:
. Them superposition produces on intervals zÎ(1,+¥) şi zÎ(-¥, -1) the following potential: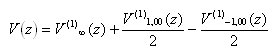 (2)
(2)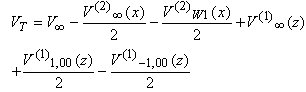 (3)
(3)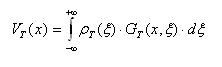 (4)
(4)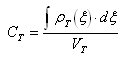 (5)
(5)