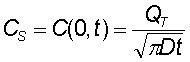ANALYTICAL SOLUTIONS TO FICK'S LAWS

In order to solve Fick's laws and find the formula for the concentration, boundary conditions are required (the value of concentration is known for some conditions (x,t), usually at the surface, initial time, etc.) . Two cases are important, and solutions can be calculated for these two cases:

• Infinite source - the source of impurities is infinite
  • the diffusion in this case is called predeposition diffusion

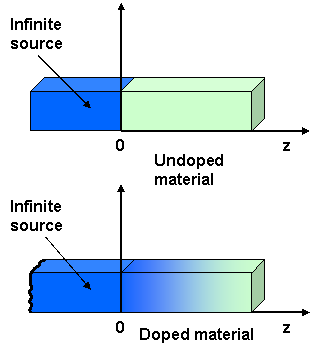
• The boundary conditions for infinite source can be written: ,
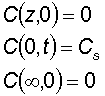  • where C_s is the fixed surface concentration, and is constant at any moment in time, due to the fact that the source is infinite and it cannot get depleted during the diffusion process.
  • Furthermore inititially the material was completely undoped, thus at t = 0 the concentration is zero.
  • Also it is considered that the material in which diffusion takes place is infinitely long, thus the concentration at its other end will always be zero, and the impurities can diffuse infinitely, without the possibility of agglomerating.
• The calculated solution is then:
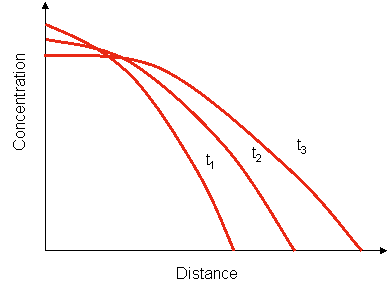
• The solution can be represented in a graph as a function of distance for different periods of time: 

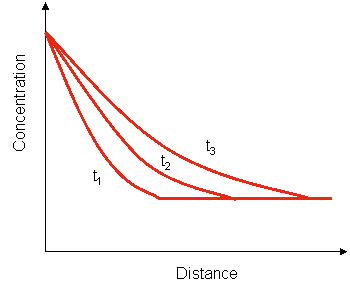
• The area below each graph (calculated by integrating the concentration) represents the total impurity that passed into material:
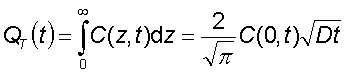
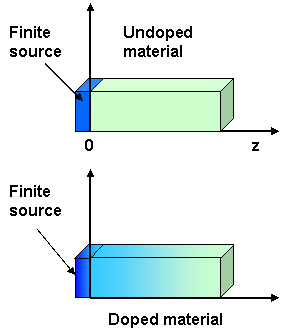
• Finite source - the source of impurities is finite
• the diffusion in this case is called drive in diffusion

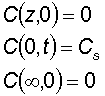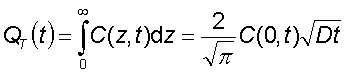
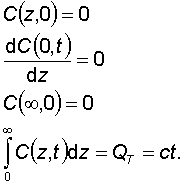• The boundary conditions for finite source can be written: , where Q_T is the total concenttration that passes into the material, and is constant, independent of time. Also in this case the material is initial undoped and infinitely long.
• The calculated solution of the impurity profile is then:
• The plot of the concentration profile at different moments in time:

• The area under each curve in the graph is constant.
• For finite source, the total concentration is constant, and the surface concentration varies in time. It can be calculated as: