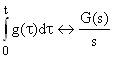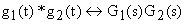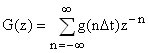|
|
||
|
Laplace transform (unilateral) of a function g(t)
s ... complex variable (s = s + jw) Shorthand notation: g(t) ↔ G(s) Key properties of
* ... convolution Z-transform
z ... complex variable z-transform bears the same kind of relationship to the discrete time Fourier transform as the It has similar properties with respect to difference equations as the z-transform can be seen as a shorthand notation for Properties of z-transform:
Related Gregorian, R., Temes G. C., Analog MOS integrated circuits for signal processing, Wiley, 1986. Johns, D. A., Martin, K., Analog integrated circuit design, Wiley, 1997. Razavi, B., RF Microelectronics, Prentice Hall, 1998. Bendat, J. S., Piersol, A. G., Random Data: Analysis & Measurement Procedures, J. Wiley, 2000.
|
 Analogue filter
Analogue filter
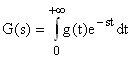 = L(g(t))
= L(g(t))